Perspective-n-Point (PnP)

Perspective-n-Point (PnP) is used to match 2D image points to 3D points, e.g 3D points are mapped from last frame to world coordinate space. 2D points are available in current frame, we try to estimate motion based on the paired points from current frame 2D points to 3D world coordinates.

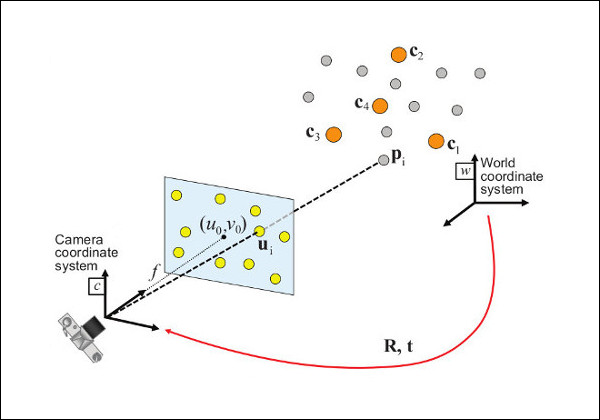
Given a mapping 2d points and 3d points, find the $t_{0:11}$ with following constriant.

\[\begin{align*} s \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} &= \bf{K} \hspace{0.1em} \Pi \hspace{0.2em} ^{c}\bf{T}_w \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} &= \begin{bmatrix} t_0 & t_1 & t_2 & t_3\\ t_4 & t_5 & t_6 & t_7\\ t_8 & t_9 & t_{10} & t_{11}\\ \end{bmatrix} \begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ 1 \end{bmatrix} \end{align*}\]

where $u$ and $v$ are image coordiantes, and $X_w$,$Y_w$,$Z_w$ are world coordiantes. $T_w$ are geometrical transformation from world coordinate system to camera coordinate system. $\hspace{0.1em} \Pi \hspace{0.2em} ^{c}$ maps 3d coordiantes to image plane, and $K$ is camera matrix mapping coordinate in image plane to pixel cordinate. $s$ is the scale parameter making sure that last row can be elimenated easily.

The most intuitive way to solve PnP is bundle adjustment (BA) to minimize $L_2$ error of projected points.

Direct Linear Tranformation

Reformulate the constriant and find direct relation bwtween image coordiante and world coordiante.

\[u = \frac{t_0X_w+t_1Y_w + t_2Z_w + t_3}{t_8X_w + t_9Y_w + t_{10}Z_w + t_{11}}\] \[v = \frac{t_4X_w+t_5Y_w + t_6Z_w + t_7}{t_8X_w + t_9Y_w + t_{10}Z_w + t_{11}}\]

then an formular of puting $t_{0:11}$ can be transformed:

\(Mt_{0:11} = 0\) where M only contains elements of image coordiantes and world coordiantes.

least squares are not here to solve a equation with right being zero, but direct linear transformation can.

$M$ has 12 elements in a rows and 2 elements in columns (12x2), thus at least 6 points are necessary to estimate $t_{0:11}$.

However, result of DLT is not perfect under constraints of $T_w$, such as rotation matrix constraints. Take upper-left 3 by 3 of $T_w$ to be R, using QR decomposition to reformulate R:

\[R = (R^{-1}R)^{1/2}R\]

to for force R being valid.

Bundle Adjustment

TODO

Variants of PnP Solvers

• P3P takes exactly 3 Points to estimate $T_w$, compared to DLT, it takes advantage the geometric edges relation.
• RANSAC PnP predict $T_w$ under RANSAC framework to get rid of outliers.
• Efficient PnP (EPnP) requires at least 4 points.
• SQPnP garantees the the global minima while keeping computation cost low.